巨大的斐波那契数！ Colossal Fibonacci Numbers!

题面翻译

输入两个非负整数 $a, b$ 和正整数 $n(0 \le a, b < 2^{64}，1 \le n \le 10^3)$ ，求 $f(a ^ b) \bmod n$ 的值, 其中 $f_0 = 0, f1 = 1, f{i + 2} = fi + f{i + 1}(i\ge 0)$。

题目描述

PDF

输入格式

输出格式

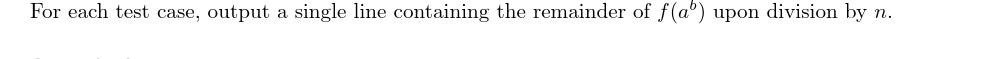
样例 #1

样例输入 #1

3
1 1 2
2 3 1000
18446744073709551615 18446744073709551615 1000

样例输出 #1

1
21
250

这道题做的有点迷

不难看出，由于答案要求取模，所以可以看穿这道题的重点在于循环节的寻找，当我们找到循环节的时候，我们就可以通过快速幂 || 取模运算快速求出答案

我的想法1.0【十分睿智】

由于 $n$ 的取值小于 $1000$ ，所以我睿智的认为只要将 $\pmod{1000}$ 意义下的斐波那契数列的循环节找到，在最后输出答案时对答案 $\pmod{n}$ 即可

$$
\texttt{\color{#66CCFF}{然后我错了……}}
$$

我睿智地发现：$1000≡0 (mod 1000)$，然而 $1000≡1 (mod 999)$

于是……

$\texttt{\color{white}\colorbox{red}{WA}}$ $\texttt{\color{white}\colorbox{red}{WA}}$ $\texttt{\color{white}\colorbox{red}{WA}}$ $\texttt{\color{white}\colorbox{red}{WA}}$

我的想法 2.0【真的是正解】

那么我们只能对每个 $n$ 单独打表……

于是……【手动滑稽】

我惊奇的发现……这张表，太大了……

所以……我把我的打表程序做成函数加进来了……

伪代码长这个样子：

int biao[1010][3010];
bool vis[1100][1100];
inline void mdzz() {
    //  int maxn=0;
    for (int cao = 1; cao <= 1000; cao++) {
        //  printf("{0,1");
        biao[cao][1] = biao[cao][2] = 1;
        for (int i = 2;; i++) {
            biao[cao][i] = biao[cao][i - 1] + biao[cao][i - 2];
            biao[cao][i]
            //  printf("
            if (vis[biao[cao][i]][biao[cao][i - 1]] == 1) {
                //  printf("
                //      maxn=max(maxn,i-2);
                break;
            }
            vis[biao[cao][i]][biao[cao][i - 1]] = 1;
        }
        memset(vis, 0, sizeof(vis));
        //  printf("},\n");
        //  printf(",");
    }
    //  printf("
    return;
}

于是我就可以轻松的通过这道题目

$\texttt{\color{white}\colorbox{green}{AC}}$ $\texttt{\color{white}\colorbox{green}{AC}}$ $\texttt{\color{white}\colorbox{green}{AC}}$ $\texttt{\color{white}\colorbox{green}{AC}}$